Phương pháp giải:

- Biến đổi phương trình về \(m = f\left( x \right)\).

- Xét hàm \(y = f\left( x \right)\) và sử dụng mối quan hệ giữa số nghiệm của phương trình với số giao điểm của đồ thị hàm số với đường thẳng tìm \(m\).

Sử dụng công thức đạo hàm \({\left( {\left| u \right|} \right)^\prime } = \dfrac{u}{{\left| u \right|}}\)

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm: \(\dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + \dfrac{{x + 3}}{{x + 4}} = \left| {x + 1} \right| - x + m\,\,\,\,\,\left( * \right)\)

Điều kiện: \(x \in \mathbb{R}\backslash \left\{ { - 1\,; - 2\,; - 3\,; - 4} \right\}\).

Từ \(\left( * \right)\) ta có \(m = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + \dfrac{{x + 3}}{{x + 4}} + x - \left| {x + 1} \right|\).

Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị \(y = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + \dfrac{{x + 3}}{{x + 4}} + x - \left| {x + 1} \right|\) và đường thẳng \(y = m\).

Xét hàm số \(y = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + \dfrac{{x + 3}}{{x + 4}} + x - \left| {x + 1} \right|\)

Ta có \(y' = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 3} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 4} \right)}^2}}} + 1 - \dfrac{{x + 1}}{{\left| {x + 1} \right|}}\)

Nhận thấy \(\left| {x + 1} \right| > x + 1\,\,\forall x \ne  - 1 \Rightarrow \left| {x + 1} \right| - \left( {x + 1} \right) > 0\,\,\forall x \ne  - 1\).

Do đó \(y' = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 3} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 4} \right)}^2}}} + \dfrac{{\left| {x + 1} \right| - \left( {x + 1} \right)}}{{\left| {x + 1} \right|}} > 0\)\(\,\,\forall x \in \mathbb{R}\backslash \left\{ { - 1\,; - 2\,; - 3\,; - 4} \right\}\).

Ta có BBT của hàm số  \(y = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + \dfrac{{x + 3}}{{x + 4}} + x - \left| {x + 1} \right|\)

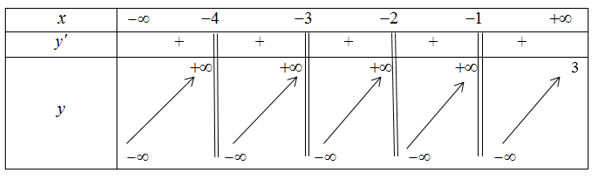
Từ bảng biến thiên, để phương trình có 4 nghiệm phân biệt thì \(m \ge 3\).

Chọn D.