Câu hỏi
Cho hình trụ có chiều cao bằng \(3\sqrt 2 \). Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng \(12\sqrt 2 \). Diện tích xung quanh của hình trụ đã cho bằng
- A \(6\sqrt {10} \pi \)
- B \(6\sqrt {34} \pi \)
- C \(3\sqrt {10} \pi \)
- D \(3\sqrt {34} \pi \)
Phương pháp giải:
Tính bán kính hình trụ và sử dụng công thức \(S = 2\pi Rh\) để tính diện tích xung quanh.
Lời giải chi tiết:
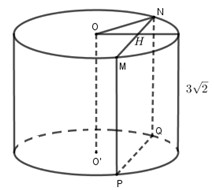
Ta có : \({S_{MMNQP}} = MN.MP = 12\sqrt 2 \)\( \Rightarrow MN = 12\sqrt 2 :3\sqrt 2 = 4\) \( \Rightarrow MH = \dfrac{1}{2}MN = \dfrac{4}{2} = 2\).
Tam giác \(ONH\) vuông tại \(H\) có \(OH = 1,NH = 2 \Rightarrow ON = \sqrt {O{H^2} + N{H^2}} = \sqrt 5 \)
\( \Rightarrow {S_{xq}} = 2\pi Rh = 2\pi \sqrt 5 .3\sqrt 2 = 6\sqrt {10} \pi \).
Chọn A.
Câu hỏi trước
