Lời giải chi tiết:

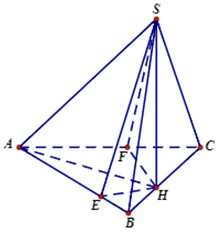
Kẻ\(SH \bot BC\) ta có \(\left( {SBC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\).

Trong \(\left( {ABC} \right)\) kẻ \(HE \bot AB;\,\,\,HF \bot AC\,\,\left( {E \in AB,\,\,F \in AC} \right)\).

Ta có \(\left\{ \begin{array}{l}AB \bot SH\,\,\left( {SH \bot \left( {ABC} \right)} \right)\\AB \bot HE\end{array} \right. \Rightarrow AB \bot \left( {SHE} \right) \Rightarrow AB \bot SE\)

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \supset SE \bot AB\\\left( {ABC} \right) \supset HE \bot AB\end{array} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABC} \right)} \right) = \angle \left( {SE;HE} \right) = \angle SEH = {60^0}\).

CMTT ta có \(SF \bot AC\) và \(\angle SFH = {60^0}\).

\( \Rightarrow \Delta SEH = \Delta SFH \Rightarrow HE = HF \Rightarrow AH\) là phân giác của \(\angle BAC\) (tính chất đường phân giác).

\( \Rightarrow AEHF\) là hình vuông (Tứ giác có 3 góc vuông và có 1 đường chéo là phân giác của 1 góc).

Xét tam giác vuông \(ABC:\,\,BC = \sqrt {A{B^2} + A{C^2}}  = a\sqrt 5 \).

Áp dụng định lí đường phân giác ta có: \(\dfrac{{HB}}{{HC}} = \dfrac{{AB}}{{AC}} = \dfrac{1}{2} \Rightarrow HB = \dfrac{{a\sqrt 5 }}{3};\,\,HC = \dfrac{{2a\sqrt 5 }}{3}\).

Áp dụng định lí cosin trong tam giác \(ABH\) có:

\(\begin{array}{l}B{H^2} = A{B^2} + A{H^2} - 2AB.AH.\cos \angle BAH\\ \Leftrightarrow \dfrac{{5{a^2}}}{9} = {a^2} + A{H^2} - 2a.AH.\dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow A{H^2} - a\sqrt 2 .AH + \dfrac{{4{a^2}}}{9} = 0 \Leftrightarrow \left[ \begin{array}{l}AH = \dfrac{{2\sqrt 2 }}{3}a\\AH = \dfrac{{\sqrt 2 a}}{3}\end{array} \right.\end{array}\)

TH1: \(AH = \dfrac{{2\sqrt 2 a}}{3} \Rightarrow HE = \dfrac{{2a}}{3} \Rightarrow SH = HE.tan{60^0} = \dfrac{{2a\sqrt 3 }}{3}\).

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{2a\sqrt 3 }}{3}.\dfrac{1}{2}.a.2a = \dfrac{{2\sqrt 2 {a^3}}}{9}\)

TH2: \(AH = \dfrac{{\sqrt 2 a}}{3} \Rightarrow HE = \dfrac{a}{3} \Rightarrow SH = HE.tan{60^0} = \dfrac{{a\sqrt 3 }}{3}\).

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.a.2a = \dfrac{{\sqrt 3 {a^3}}}{9}\)

Chọn C.