Phương pháp giải:

+) Kẻ \(SH \bot BC\). Chứng minh \(SH \bot \left( {ABC} \right)\).

+) Chứng minh \(H\) là trung điểm của \(AC\), tính \(SH\).

+) Áp dụng công thức tính thể tích \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}}\).

Lời giải chi tiết:

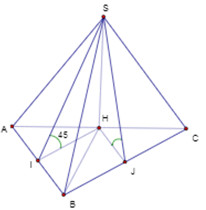
Kẻ \(SH \bot BC\). Vì \(\left( {SAC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\).

Gọi \(I,\,\,J\) là hình chiếu của \(H\) lên \(AB,\,\,BC\) ta có:

\(\left\{ \begin{array}{l}AB \bot SH\,\,\left( {SH \bot \left( {ABC} \right)} \right)\\AB \bot HI\end{array} \right. \Rightarrow AB \bot \left( {SHI} \right) \Rightarrow AB \bot SI\).

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\\\left( {ABC} \right) \supset HI \bot AB\end{array} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABC} \right)} \right) = \angle SIH = {45^0}\).

CMTT ta có \(BC \bot SJ\) và \(\angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle SJH = {45^0}\).

\( \Rightarrow \Delta SIH,\,\,\Delta SJH\) là các tam giác vuông cân tại \(H \Rightarrow SH = IH = JH\).

Ta có \(\left\{ \begin{array}{l}HI \bot AB,\,\,BC \bot AB \Rightarrow HI//BC \Rightarrow HI//BJ\\HJ \bot BC,\,\,AB \bot BC \Rightarrow HJ//AB \Rightarrow HJ//IB\end{array} \right.\)

\( \Rightarrow \) Tứ giác \(BIHJ\) là hình bình hành, lại có \(HI = HJ\,\,\left( {cmt} \right) \Rightarrow BIHJ\) là hình thoi.

\( \Rightarrow BH\) là phân giác của \(\angle ABC \Rightarrow BH\) đồng thời là trung tuyến (Do tam giác \(ABC\) vuông cân tại \(B\))

\( \Rightarrow H\) là trung điểm của \(AC\) \( \Rightarrow HI\) là đường trung bình của tam giác \(ABC \Rightarrow HI = \dfrac{1}{2}BC = \dfrac{a}{2}\).

\( \Rightarrow SH = \dfrac{a}{2};\,\,{S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{{{a^2}}}{2}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{{12}}\).

Chọn A.