Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt bên \(SAB\) là tam giác vuông tại \(S\) vàa ằm trong mặt phẳng vuông góc với đáy, hình chiếu vuông góc của \(S\) trên đường thẳng \(AB\) là điểm \(H\) thuộc đoạn \(AB\) sao cho \(BH = 2AH\). Tính thể tích khối chóp \(S.ABCD\).
- A \(\dfrac{{{a^3}\sqrt 3 }}{3}\)
- B \(\dfrac{{{a^3}\sqrt 2 }}{3}\)
- C \(\dfrac{{{a^3}\sqrt 2 }}{9}\)
- D \(\dfrac{{{a^3}\sqrt 3 }}{9}\)
Phương pháp giải:
+) Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) tính \(SH\).
+) \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\).
Lời giải chi tiết:
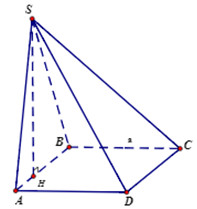
Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có
\(S{H^2} = HA.HB = \dfrac{a}{3}.\dfrac{{2a}}{3} = \dfrac{{2{a^2}}}{9} \Leftrightarrow SH = \dfrac{{a\sqrt 2 }}{3}\).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{3}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{9}\).
Chọn C.
Câu hỏi trước
