Câu hỏi
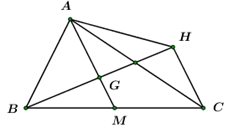
Cho tam giác ABC. Gọi H là điểm đối xứng với B qua G với G là trọng tâm tam giác. Chọn khẳng định đúng?
- A \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)
- B \(\overrightarrow {CH} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
- C Cả A, B đều đúng
- D Cả A, B đều sai
Phương pháp giải:
Áp dụng quy tắc hình bình hành, quy tắc trung điểm để tách và rút gọn.
Lời giải chi tiết:
Áp dụng quy tắc hình bình hành ta có:
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {AH} = 2\overrightarrow {AG} \\ \Rightarrow \overrightarrow {AH} = 2\overrightarrow {AG} - \overrightarrow {AB} = \frac{2}{3}\overrightarrow {AM} - \overrightarrow {AB} \\ = \frac{2}{3}\left( {\overrightarrow {AC} + \overrightarrow {AB} } \right) - \overrightarrow {AB} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \\ \Rightarrow \overrightarrow {CH} = \overrightarrow {AH} - \overrightarrow {AC} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} .\end{array}\)
Chọn C.