Phương pháp giải:

+) Vẽ đồ thị hàm số \(y = f\left( x \right)\).

+) Suy ra đồ thị hàm số \(y = g\left( x \right) = f\left( {\left| x \right|} \right) + m\) và biện luận.

Lời giải chi tiết:

TXĐ : \(D = \mathbb{R}\). Ta có \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = 2 \Rightarrow y =  - 4\end{array} \right.\).

Ta vẽ được đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2}\)như sau:

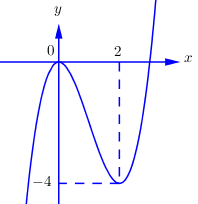
Đồ thị hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right) + m\) được tạo ra từ đồ thị hàm số \(y = f\left( x \right)\) như sau:

+) Lấy đối xứng phần đồ thị bên phải trục \(Ox\) qua trục \(Ox\).

+) Xóa đi phần đồ thị bên trái trục \(Ox\).

+) Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang trái theo chiều của trục \(Ox\) một lượng \(m\) đơn vị.

Khi đó ta có đồ thị hàm số \(y = g\left( x \right) = f\left( {\left| x \right|} \right) + m\) như sau:

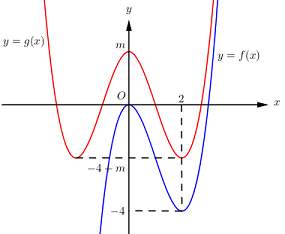
Để đồ thị hàm số \(g\left( x \right) = f\left( {\left| x \right| + m} \right)\) cắt trục hoành tại 4 điểm phân biệt thì \(m\left( { - 4 + m} \right) < 0 \Leftrightarrow 0 < m < 4\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3} \right\}\).

Vậy tổng các giá trị của \(m\) là \(1 + 2 + 3 = 6\).

Chọn D