Câu hỏi
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(V\). Tính diện tích khối đa diện \(BAA'C'C\).
- A \(\dfrac{{3V}}{4}\)
- B \(\dfrac{{2V}}{3}\)
- C \(\dfrac{V}{2}\)
- D \(\dfrac{V}{4}\)
Phương pháp giải:
Phân chia khối đa diện.
Lời giải chi tiết:
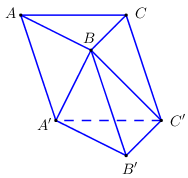
Ta có: \({V_{ABC.A'B'C'}} = {V_{BAA'C'C}} + {V_{B.A'B'C'}}\).
\(\dfrac{{{V_{B.A'B'C'}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}d\left( {B;\left( {A'B'C'} \right)} \right).{S_{\Delta A'B'C'}}}}{{d\left( {B;\left( {A'B'C'} \right)} \right).{S_{\Delta A'B'C'}}}} = \dfrac{1}{3}\).
Vậy \({V_{BAA'C'C}} = {V_{ABC.A'B'C'}} - {V_{B.A'B'C'}} = {V_{ABC.A'B'C'}} - \dfrac{1}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{{2V}}{3}\).
Chọn B
Câu hỏi trước
