Câu hỏi
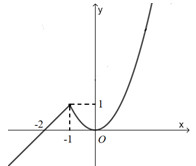
Cho hàm số \(y = f\left( x \right)\) có đồ thị gồm một phần đường thẳng và một phần đường parabol có đỉnh là gốc tọa độ O như hình vẽ. Giá trị của \(\int\limits_{ - 3}^3 {f\left( x \right)dx} \) bằng
- A \(\dfrac{{26}}{3}.\)
- B \(\dfrac{{38}}{3}.\)
- C \(\dfrac{4}{3}.\)
- D \(\dfrac{{28}}{3}.\)
Phương pháp giải:
Xác định hàm số \(f\left( x \right)\) và tính tích phân.
Lời giải chi tiết:
Ta có: \(f\left( x \right) = \left\{ \begin{array}{l}x + 2\,\,khi\,\,x \le - 1\\{x^2}\,\,khi\,\,x \ge - 1\end{array} \right.\)
\(\begin{array}{l}\int\limits_{ - 3}^3 {f\left( x \right)dx} = \left( {\int\limits_{ - 3}^{ - 2} {f\left( x \right)dx} + \int\limits_{ - 2}^1 {f\left( x \right)dx} } \right) + \int\limits_{ - 1}^3 {f\left( x \right)dx} \\ = \int\limits_{ - 3}^{ - 1} {\left( {x + 2} \right)dx} + \int\limits_{ - 1}^3 {{x^2}dx} = \left. {\left( {\dfrac{{{x^2}}}{2} + 2x} \right)} \right|_{ - 3}^{ - 1} + \left. {\dfrac{1}{3}{x^3}} \right|_{ - 1}^3 = - \dfrac{3}{2} + \dfrac{3}{2} + 9 + \dfrac{1}{3} = \dfrac{{28}}{3}\end{array}\).
Chọn: D







