Câu hỏi
Cho hàm số \(y = a{x^4} + b{x^2} + c\), \(a \ne 0\) có đồ thị như hình vẽ.
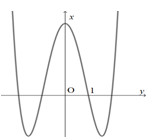
Mệnh đề nào dưới đây đúng
- A \(f'\left( { - \dfrac{1}{2}} \right) = - 2\).
- B \(f'\left( { - \dfrac{1}{2}} \right) > 0\).
- C \(f'\left( { - \dfrac{1}{2}} \right) = 0\).
- D \(f'\left( { - \dfrac{1}{2}} \right) < 0\).
Phương pháp giải:
Quan sát và rút ra tính đơn điệu của hàm số trên khoảng \(\left( { - 1;0} \right)\). Từ đó, đánh giá \(f'\left( { - \dfrac{1}{2}} \right)\).
Lời giải chi tiết:
Nhận xét: Hàm số đồng biến trên \(\left( { - 1;0} \right)\) và không có cực trị tại \( - \dfrac{1}{2}\)\( \Rightarrow f'\left( { - \dfrac{1}{2}} \right) > 0.\)
Chọn: B
Câu hỏi trước
