Câu hỏi
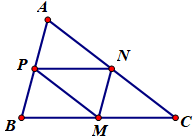
Cho tam giác \(ABC\). Gọi M, N, P lần lượt là trung điểm của \(BC,\,\,CA,\,\,AB\). \(O\) là điểm bất kì. Khẳng định nào sau đây là đúng nhất?
- A \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \)
- B \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {MN} + \overrightarrow {MP} \)
- C \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \)
- D \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \)
Phương pháp giải:
Chứng minh \(\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \), từ đó sử dụng quy tắc cộng để tách và nhóm cho phù hợp.
Lời giải chi tiết:
Vì \(PN,\,MN\) là đường trung bình của tam giác \(ABC\) nên
\(PN//BM,\,\,MN//BP\) suy ra tứ giác \(BMNP\) là hình bình hành
\( \Rightarrow \overrightarrow {BM} = \overrightarrow {PN} \)
\(N\) là trung điểm của \(AC \Rightarrow \overrightarrow {CN} = \overrightarrow {NA} \)
Do đó theo quy tắc ba điểm ta có
\(\begin{array}{l}\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \left( {\overrightarrow {PN} + \overrightarrow {NA} } \right) + \overrightarrow {AP} \\ = \overrightarrow {PA} + \overrightarrow {AP} = \overrightarrow 0 \end{array}\)
Theo quy tắc ba điểm ta có
\(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OP} + \overrightarrow {PA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) + \overrightarrow {PA} + \overrightarrow {MB} + \overrightarrow {NC} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) - \left( {\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} } \right)\end{array}\)
Mà \(\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \) suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Chọn D.