Câu hỏi
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB{\rm{ = 2,}}\,AC = 4.\) Giá trị của \(\left| {2.\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng
- A \(4\sqrt 2 \)
- B \(8\)
- C \(4\)
- D \(8\sqrt 2 \)
Phương pháp giải:
Vẽ hình, xác định vectơ bài cho rồi tính độ dài vecto bài yêu cầu.
Lời giải chi tiết:
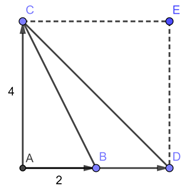
Dựng \(D\) sao cho \(2\overrightarrow {AB} = \overrightarrow {AD} \).
Khi đó, \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = 4\) nên \(\Delta ACD\) là tam giác vuông cân tại \(D\)
Dựng \(E\) sao cho tứ giác \(ACED\) là hình vuông.
Khi đó \(\left| {2\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE = CD\)
Mà \(C{D^2} = 2A{C^2} = {2.4^2} = 32 \Rightarrow CD = 4\sqrt 2 \)
Chọn A.
Câu hỏi trước
