Câu hỏi
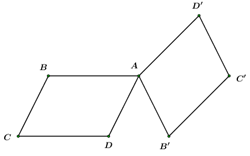
Cho hai hình bình hành \(ABCD\) và \(AB'C'D'\) có chung đỉnh A. Khẳng định nào đúng
- A \(\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {AC} \)
- B \(\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow 0 \)
- C \(\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BC} \)
- D \(\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BD} \)
Phương pháp giải:
Sử dụng quy tắc trừ và quy tắc hình bình hành để tách và nhóm cho phù hợp.
Lời giải chi tiết:
Theo quy tắc trừ và quy tắc hình bình hành ta có:
\(\begin{array}{l}\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \left( {\overrightarrow {AB} - \overrightarrow {AB'} } \right) + \left( {\overrightarrow {AC'} - \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD} - \overrightarrow {AD'} } \right)\\ = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) - \overrightarrow {AC} - \left( {\overrightarrow {AB'} + \overrightarrow {AD} '} \right) + \overrightarrow {AC'} = \overrightarrow 0 \end{array}\)
Chọn B.