Câu hỏi
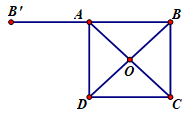
Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). \(M\) là một điểm bất kỳ. Tính độ dài vectơ \(\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} \)
- A \(\left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = a\)
- B \(\left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = 3a\)
- C \(\left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = 2a\)
- D \(\left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = \frac{{3a}}{2}\)
Phương pháp giải:
Lấy\(B'\) là điểm đối xứng của \(B\) qua \(A\). Áp dụng quy tắc trừ để tính.
Lời giải chi tiết:
Áp dụng quy tắc trừ ta có:
\(\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) - \left( {\overrightarrow {MC} - \overrightarrow {MD} } \right) = \overrightarrow {BA} - \overrightarrow {DC} = \overrightarrow {BA} - \overrightarrow {DC} \)
Lấy\(B'\) là điểm đối xứng của \(B\) qua \(A\)
Khi đó \( - \overrightarrow {DC} = \overrightarrow {AB'} \Rightarrow \overrightarrow {BA} - \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB'} = \overrightarrow {BB'} \)
\( \Rightarrow \left| {\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} + \overrightarrow {MD} } \right| = \left| {\overrightarrow {BB'} } \right| = BB' = 2a\)
Chọn C.