Câu hỏi
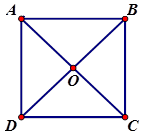
Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|,\,\,\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right|,\,\,\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right|\)
- A \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 2 \)
- B \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right| = {{a\sqrt 2 } \over 2}\)
- C \(\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right| = a\sqrt 2 \)
- D Cả A, B, C đều đúng
Phương pháp giải:
Áp dụng quy tắc hình bình hành, quy tắc cộng trừ để tính.
Lời giải chi tiết:
+ Theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\).
Áp dụng định lí Pitago ta có \(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = \sqrt 2 a\)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 2 \)
+ Vì O là tâm của hình vuông nên \(\overrightarrow {OA} = \overrightarrow {CO} \Rightarrow \overrightarrow {OA} - \overrightarrow {CB} = \overrightarrow {CO} - \overrightarrow {CB} = \overrightarrow {BO} \)
Vậy \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right| = \left| {\overrightarrow {BO} } \right| = BO = {1 \over 2}BD = {1 \over 2}AC = {{a\sqrt 2 } \over 2}.\)
+ Do \(ABCD\) là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \Rightarrow \overrightarrow {CD} - \overrightarrow {DA} = \overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \)
Mà \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 2 \) suy ra \(\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right| = a\sqrt 2 \)
Chọn D.