Câu hỏi
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân đỉnh \(A\), \(AB = a\sqrt 2 \). Gọi \(I\) là trung điểm của \(BC\), hình chiếu vuông góc \(H\) của \(S\) trên mặt đáy \((ABC)\) thỏa mãn \(\overrightarrow {IA} = - 2\overrightarrow {IH} \). Khoảng cách từ điểm \(B\) đến \((SAI)\) là:
- A \(a\)
- B \(2a\)
- C \(\dfrac{{a\sqrt 2 }}{2}\)
- D \(a\sqrt 2 \)
Phương pháp giải:
+) Xác định vị trí điểm H.
+) Chứng minh \(BC \bot \left( {SAI} \right)\).
Lời giải chi tiết:
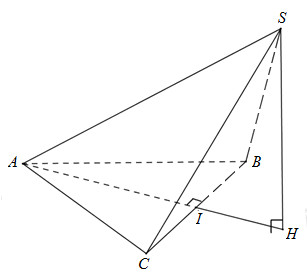
Vì tam giác ABC vuông cân tại A nên \(AI \bot BC\) và \(BC = AB\sqrt 2 = 2a\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AI\\BC \bot SH\left( {SH \bot \left( {ABC} \right)} \right)\end{array} \right.\\ \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow d\left( {B;\left( {SAI} \right)} \right) = BI = \dfrac{1}{2}BC = a\end{array}\)
Chọn A.
Câu hỏi trước
