Phương pháp giải:

+) Gọi H là tâm của tam giác đều ABC \( \Rightarrow A'H \bot \left( {ABC} \right)\)

+) Xác định khoảng cách từ 1 điểm đến mặt phẳng chứa đường cao.

Lời giải chi tiết:

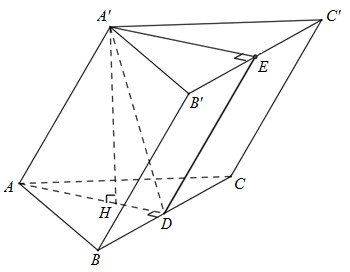
Vì chóp \(A'.ABC\)là chóp đều nên ABC là tam giác đều

Gọi H là tâm của tam giác đều ABC \( \Rightarrow A'H \bot \left( {ABC} \right)\)

\(\left( {A'AD} \right) \cap B'C' = E \Rightarrow d\left( {C';\left( {A'AD} \right)} \right) = d\left( {C';\left( {A'ADE} \right)} \right)\)\(\left( {A'ADE} \right) \cap \left( {BCC'B'} \right) = DE \Rightarrow DE//BB'\). Mà D là trung điểm của BC nên E là trung điểm của \(B'C'\)

Tam giác \(A'B'C'\) đều nên trung tuyến \(A'E\) đồng thời là đường cao \( \Rightarrow A'E \bot B'C'\) 

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}C'E \bot A'E\\C'E \bot A'H\left( {A'H \bot \left( {A'B'C'} \right)} \right)\end{array} \right\} \Rightarrow C'E \bot \left( {A'ADE} \right)\\ \Rightarrow d\left( {C';\left( {A'ADE} \right)} \right) = C'E = \dfrac{{B'C'}}{2} = \dfrac{a}{2}\end{array}\)

Chọn D.