Câu hỏi
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang cân với hai đáy \(BC\) và \(AD\). Biết \(AD = 2a,\) \(AB = BC = CD = a\) và hình chiếu vuông góc của \(S\) xuống \((ABCD)\) trùng với trung điểm của cạnh \(AD\). Gọi \(E\) là trung điểm của \(BC\). Khoảng cách từ \(E\) đến \((SAD)\) là:
- A \(\dfrac{{a\sqrt 3 }}{2}\)
- B \(\dfrac{a}{2}\)
- C \(\dfrac{{a\sqrt 3 }}{3}\)
- D \(a\)
Phương pháp giải:
Xác định khoảng cách từ 1 điểm đến mặt phẳng chứa đường cao.
Lời giải chi tiết:
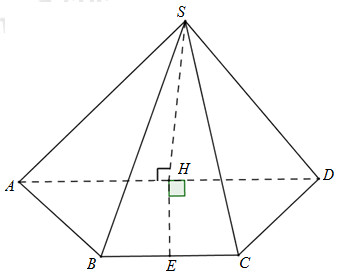
Vì H là trung điểm của AD, ABCD là hình thang cân nên E là trung điểm của BC và \(HE \bot BC\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}EH \bot SH\left( {SH \bot \left( {ABCD} \right)} \right)\\EH \bot AD\,\,\,\left( {AD//BC} \right)\end{array} \right.\\ \Rightarrow EH \bot \left( {SAD} \right) \Rightarrow d\left( {E;\left( {SAD} \right)} \right) = EH\end{array}\)
Trong (ABCD) kẻ \({\rm{BF}} \bot AD\)
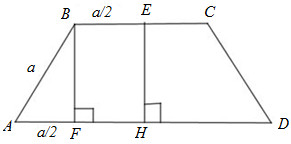
Ta có: \(AF = FH = \dfrac{{AD - AB}}{2} = \dfrac{{2a - a}}{2} = \dfrac{a}{2}\)
Xét tam giác vuông ABF có: \(BF = \sqrt {A{B^2} - A{F^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2} = HE\)
Chọn A.







