Câu hỏi
Cho hình chóp đều \(S.ABC\) có cạnh đáy bằng \(a\). Gọi \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(BC\). Khoảng cách từ \(M\) đến \((SAN)\) là:
- A \(\dfrac{a}{2}\)
- B \(\dfrac{a}{3}\)
- C \(\dfrac{a}{4}\)
- D \(\dfrac{a}{5}\)
Phương pháp giải:
+) Gọi O là tâm tam giác đều ABC \( \Rightarrow SO \bot \left( {ABC} \right)\)
+) Xác định khoảng cách từ 1 điểm đến mặt phẳng chứa đường cao.
Lời giải chi tiết:
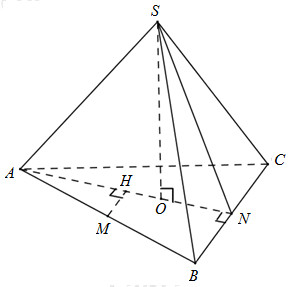
Gọi O là tâm tam giác đều ABC. Vì chóp S.ABC đều nên \(SO \bot \left( {ABC} \right)\)
Trong (ABC) kẻ \(MH \bot AN\)
Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}MH \bot AN\\MH \bot SO\left( {SO \bot \left( {ABC} \right)} \right)\end{array} \right.\\ \Rightarrow MH \bot \left( {SAN} \right) \Rightarrow d\left( {M;\left( {SAN} \right)} \right) = MH\end{array}\)
Ta có :
\(\begin{array}{l}MH \bot AN,BN \bot AN \Rightarrow MH//BN \Rightarrow \dfrac{{MH}}{{BN}} = \dfrac{{AM}}{{AB}} = \dfrac{1}{2}\\ \Rightarrow MH = \dfrac{1}{2}BN = \dfrac{1}{2}.\dfrac{a}{2} = \dfrac{a}{4}\end{array}\)
Chọn C.







