Câu hỏi
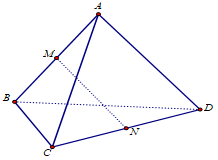
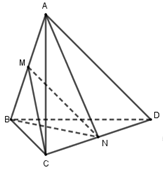
Cho khối tứ diện \(ABCD.\) Gọi \(M,N\) lần lượt là trung điểm của AB và CD (tham khảo hình vẽ bên). Đặt V là thể tích của khối tứ diện ABCD, \({V_1}\) là thể tích của khối tứ diện MNBC. Khẳng định nào sau đây đúng ?
- A \(\frac{{{V_1}}}{V} = \frac{1}{4}.\)
- B \(\frac{{{V_1}}}{V} = \frac{1}{2}.\)
- C \(\frac{{{V_1}}}{V} = \frac{1}{3}.\)
- D \(\frac{{{V_1}}}{V} = \frac{2}{3}.\)
Phương pháp giải:
Sử dụng tỉ số thể tích của khối chóp tam giác: \(\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}\).
Lời giải chi tiết:
Ta có : \(\frac{{{V_{B.MNC}}}}{{{V_{B.ANC}}}} = \frac{{BM}}{{BA}} = \frac{1}{2} \Rightarrow {V_1} = \frac{1}{2}{V_{B.ANC}}\).
Mà \(\frac{{{V_{B.ANC}}}}{{{V_{B.ACD}}}} = \frac{{CN}}{{CD}} = \frac{1}{2} \Rightarrow {V_{B.ANC}} = \frac{1}{2}{V_{ABCD}} = \frac{V}{2}\)
\( \Rightarrow {V_1} = \frac{1}{2}{V_{B.ANC}} = \frac{1}{2}.\frac{V}{2} = \frac{V}{4} \Rightarrow \frac{{{V_1}}}{V} = \frac{1}{4}\) .
Chọn A.
Câu hỏi trước
