Câu hỏi
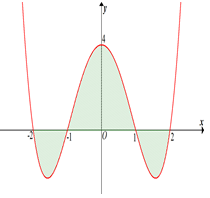
Cho hàm số \(y = f\left( x \right) = {x^4} - 5{x^2} + 4\) có đồ thị như hình vẽ bên. Gọi \(S\)là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?.
- A \(S = \int\limits_{ - 2}^2 {\left| {f\left( x \right)} \right|dx} \)
- B \(S = 2\int\limits_0^2 {\left| {f\left( x \right)} \right|dx} \)
- C \(S = 2\left| {\int\limits_0^1 {f\left( x \right)dx} } \right| + 2\left| {\int\limits_1^2 {f\left( x \right)dx} } \right|\)
- D \(S = 2\left| {\int\limits_0^2 {f\left( x \right)dx} } \right|\)
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số\(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a;x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Vì \(y = f\left( x \right) = {x^4} - 5{x^2} + 4\) là hàm trùng phương nên đồ thị hàm số nhận \(Oy\) làm trục đối xứng.
Từ hình vẽ ta có \(S = \int\limits_{ - 2}^2 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^2 {\left| {f\left( x \right)} \right|dx} = 2\int\limits_0^2 {\left| {f\left( x \right)} \right|dx} \) nên A, B đúng.
Lại có \(S = 2\left| {\int\limits_0^1 {f\left( x \right)dx} } \right| + 2\left| {\int\limits_1^2 {f\left( x \right)dx} } \right|\) nên C đúng.
Nhận thấy D sai vì trên khoảng\(\left( {0;2} \right)\) thì \(f\left( x \right)\) có đổi dấu qua \(x = 1\) nên ta không thể đưa dấu giá trị tuyệt đối ra ngoài dấu tích phân.
Chọn D.