Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh Điểm E là trung điểm của cạnh C’D’. Hai điểm M và N lần lượt thay đổi trên hai cạnh BC và CC’. Giá trị nhỏ nhất của tổng \(AM + MN + NE\) là:
- A \(\dfrac{{5a}}{2}\).
- B \(\dfrac{{\left( {2\sqrt 2 + 5\sqrt 5 } \right)a}}{2}\).
- C \(2a\).
- D \(\left( {\sqrt 2 + 1} \right)a\).
Lời giải chi tiết:
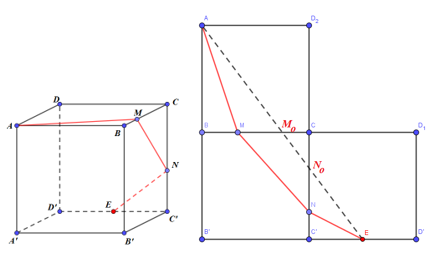
Trải các mặt (BCC’B’), (CC’DD’), (ABCD) như hình vẽ.
Ta có: \(AM + MN + NE \ge AE \Rightarrow {\left( {AM + MN + NE} \right)_{\min }} = AE\) khi và chỉ khi \(A,M,N,E\) thẳng hàng (tức là M, N trùng với \({M_0},{N_0}\) như hình vẽ).
Mà \(AE = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\dfrac{{3a}}{2}} \right)}^2}} = \sqrt {4{a^2} + \dfrac{{9{a^2}}}{4}} = \dfrac{{5a}}{2}\)\( \Rightarrow {\left( {AM + MN + NE} \right)_{\min }} = \dfrac{5}{2}a\).
Chọn: A
Câu hỏi trước
