Câu hỏi
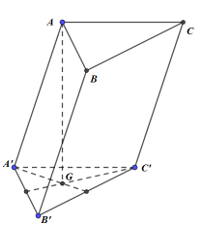
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều. Biết \(AA' = 2a,AB = a\) và hình chiếu vuông góc của \(A\) lên đáy \(\left( {A'B'C'} \right)\) là trọng tâm \(\Delta A'B'C'\). Tính thể tích khối lăng trụ.
- A \(\dfrac{{\sqrt 3 {a^3}}}{2}\).
- B \(\dfrac{{\sqrt {11} {a^3}}}{4}\).
- C \(\dfrac{{\sqrt {11} {a^3}}}{3}\).
- D \(\dfrac{{4{a^3}}}{3}\).
Phương pháp giải:
Thể tích khối trụ: \(V = Sh\).
Lời giải chi tiết:
\(\Delta ABC\) đều, \(AB = a \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4},\,\,\,GA' = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\(\Delta AA'G\) vuông tại \(G\)\( \Rightarrow AG = \sqrt {AA{'^2} - A'{G^2}} = \sqrt {4{a^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{{11}}{3}} a\)
Thể tích khối lăng trụ: \(V = \dfrac{{{a^2}\sqrt 3 }}{4}.\sqrt {\dfrac{{11}}{3}} a = \dfrac{{{a^3}\sqrt {11} }}{4}\).
Chọn: B
Câu hỏi trước
