Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(2a\), gọi \(M\) là trung điểm của \(BB'\) và \(P\) thuộc cạnh \(DD'\) sao cho \(DP = \dfrac{1}{4}DD'\). Mặt phẳng \(\left( {AMP} \right)\) cắt \(CC'\) tại \(N\). Thể tích khối đa diện \(AMNPBCD\) bằng:
- A \(2{a^3}\).
- B \(3{a^3}\).
- C \(\dfrac{{9{a^3}}}{4}\).
- D \(\dfrac{{11{a^3}}}{3}\).
Phương pháp giải:
Áp dụng công thức \(\dfrac{{{V_{AMNPBCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{BM}}{{BB'}} + \dfrac{{DP}}{{DD'}}} \right)\).
Lời giải chi tiết:
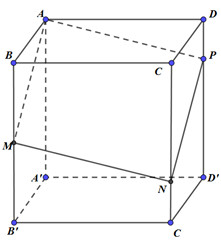
Áp dụng công thức: \(\dfrac{{{V_{AMNPBCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{BM}}{{BB'}} + \dfrac{{DP}}{{DD'}}} \right) = \dfrac{3}{8} \Rightarrow {V_{AMNPBCD}} = \dfrac{3}{8}.8{a^3} = 3{a^3}\).
Chọn: B
Câu hỏi trước
