Phương pháp giải:

Đánh giá nghiệm của phương trình qua nghiệm của đa thức \(f\left( x \right) = {x^3} - 3x + 1\).

Lời giải chi tiết:

\(y = f\left( x \right) = {x^3} - 3x + 1 \Rightarrow f'\left( x \right) = 3{x^2} - 3\,;\,f'\left( x \right) = 0 \Leftrightarrow x =  \pm 1\)

Ta có đồ thị hàm số \(y = f\left( x \right) = {x^3} - 3x + 1\) như sau:

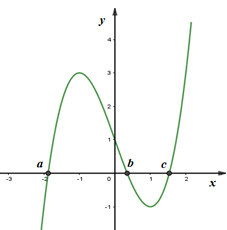
Từ đồ thị hàm số trên, có: \({\left[ {f\left( x \right)} \right]^3} - 3f\left( x \right) + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = b\\f\left( x \right) = c\end{array} \right.\), với \( - 2 < a <  - 1,\,\,0 < b < 1 < c < 2\)

Phương trình \(f\left( x \right) = a\), với \( - 2 < a <  - 1\) có 1 nghiệm.

Phương trình \(f\left( x \right) = b\), với \(0 < b < 1\) có 3 nghiệm phân biệt.

Phương trình \(f\left( x \right) = c\), với \(1 < c < 2\) có 3 nghiệm phân biệt.

Vậy, phương trình \({\left[ {f\left( x \right)} \right]^3} - 3f\left( x \right) + 1 = 0\) có 7 nghiệm phân biệt.

Chọn: B