Phương pháp giải:

Thể tích của khối cầu: \(V = \dfrac{4}{3}\pi {r^3}\).

Lời giải chi tiết:

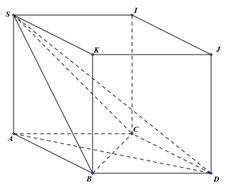
Do \(S.ABC\) có đáy là tam giác vuông cân, \(AB = AC = a,\,SA = a\) và \(SA \bot \left( {ABC} \right)\) nên \(S,A,B,C\) là 4 đỉnh của hình lập phương \(AIJK.ACDB\) (như hình vẽ)

Tâm của mặt cầu ngoại tiếp hình chóp \(S.ABC\) chính là tâm của hình lập phương. Bán kính mặt cầu đó là: \(R = \dfrac{{SD}}{2} = \dfrac{{\sqrt {{a^2} + {a^2} + {a^2}} }}{2} = \dfrac{{\sqrt 3 a}}{2}\)

Thể tích của khối cầu đó là: \(V = \dfrac{4}{3}\pi .{\left( {\dfrac{{\sqrt 3 a}}{2}} \right)^3} = \dfrac{{\sqrt 3 \pi {a^3}}}{2}\).

Chọn: B