Câu hỏi
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a tâm O, \(SO \bot \left( {ABCD} \right);SO = \dfrac{{a\sqrt 6 }}{3};\) \(OB = \dfrac{{a\sqrt 3 }}{3}\) . Tính số đo góc tạo bởi hai mặt phẳng (ABC) và (SBC)?
- A \({30^0}\)
- B \({45^0}\)
- C \({60^0}\)
- D \({90^0}\)
Phương pháp giải:
+) Kẻ \(OH \bot BC\), sử dụng phương pháp xác định góc giữa hai mặt phẳng để xác định góc giữa mặt phẳng (SBC) và (ABC).
+) Tính tan của góc vừa xác định được.
Lời giải chi tiết:
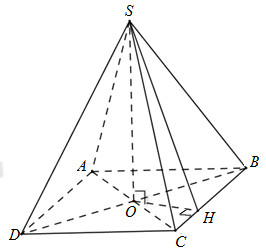
Kẻ \(OH \bot BC \Rightarrow SH \bot BC \Rightarrow \widehat {SHO} = \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)}\).
Ta có:
\(\begin{array}{l}OA = OC = \sqrt {B{C^2} - O{B^2}} = \dfrac{{a\sqrt 6 }}{3}\\\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} \Rightarrow OH = \dfrac{{a\sqrt 2 }}{3}\end{array}\)
Trong tam giác vuông SHO ta có:
\(\tan \widehat {SHO} = \dfrac{{SO}}{{OH}} = \sqrt 3 \Rightarrow \widehat {SHO} = {60^0}\)
Chọn C.







