Phương pháp giải:

Trong $\left( {SCD} \right)$ kẻ $DE \bot SC$. Chứng minh $\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {DE;BE} \right)} \Rightarrow \left[ \begin{array}{l}\widehat {DEB} = {60^0}\\\widehat {DEB} = {120^0}\end{array} \right.$

Lời giải chi tiết:

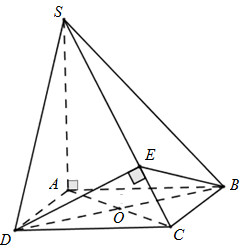
Ta có: $\left. \begin{array}{l}BD \bot SA\\BD \bot AC\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC$

Trong $\left( {SCD} \right)$ kẻ $DE \bot SC \Rightarrow SC \bot \left( {BDE} \right) \Rightarrow SC \bot BE$

$\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\DE \bot SC\\BE \bot SC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {DE;BE} \right)} = {60^0}$

$\left. \begin{array}{l}CD \bot SA\\CD \bot AD\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD$ vuông tại D

$\Rightarrow \dfrac{1}{{D{E^2}}} = \dfrac{1}{{D{C^2}}} + \dfrac{1}{{S{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}}$

Ta có: $DE = BE \Rightarrow \Delta EBD$ cân tại E

Nếu $\widehat {DEB} = {60^0} \Rightarrow \Delta EBD$đều$\Rightarrow DE = BD = a\sqrt 2$

$\Rightarrow \dfrac{1}{{2{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}} \Rightarrow \dfrac{1}{{S{A^2} + {a^2}}} =  - \dfrac{1}{{2{a^2}}}$ (vô lý)

$\Rightarrow \widehat {DEB} = {120^0} \Rightarrow \widehat {EDB} = {30^0}$

$\Delta EBD$ cân tại E, O là trung điểm của BD $\Rightarrow EO \bot BD \Rightarrow DE = \dfrac{{DO}}{{cos30}} = \dfrac{{a\sqrt 2 }}{2}\dfrac{2}{{\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}$

$\Rightarrow \dfrac{3}{{2{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}} \Rightarrow \dfrac{1}{{S{A^2} + {a^2}}} = \dfrac{1}{{2{a^2}}} \Rightarrow S{A^2} + {a^2} = 2{a^2} \Rightarrow S{A^2} = {a^2} \Rightarrow SA = a$

Chọn A.