Phương pháp giải:

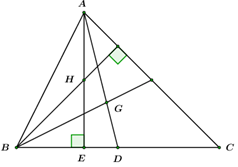
+) Gọi \(D\) là trung điểm của \(BC,\,\,E\) là chân đường vuông góc của \(A\) trên \(BC.\)

+) Áp dụng tính chất trọng tâm tam giác ta có: \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AD}  \Rightarrow \) tọa độ điểm \(D.\)

+) Lập phương trình đường thẳng \(BC\) đi qua \(D\) và vuông góc với \(AH,\) nhận \(\overrightarrow {AH} \) làm VTPT.

+) Gọi tọa độ điểm \(B,\,\,C\) thuộc đường thẳng \(BC.\)

+) Khi đó ta có: \(BH \bot AC \Rightarrow \overrightarrow {BH} .\overrightarrow {AC}  = 0 \Rightarrow \) tọa độ điểm \(B.\)

Lời giải chi tiết:

Gọi \(D\) là trung điểm của \(BC,\,\,E\) là chân đường vuông góc của \(A\) trên \(BC.\)

Áp dụng tính chất trọng tâm tam giác ta có:

\(\begin{array}{l}\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AD}  \Leftrightarrow \left( {\frac{{13}}{3};\, - \frac{{11}}{3}} \right) = \frac{2}{3}\left( {{x_D} + 3;\,\,{y_D} - 6} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{{13}}{3} = \frac{2}{3}\left( {{x_D} + 3} \right)\\ - \frac{{11}}{3} = \frac{2}{3}\left( {{y_D} - 6} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = \frac{7}{2}\\{y_D} = \frac{1}{2}\end{array} \right. \Rightarrow D\left( {\frac{7}{2};\,\,\frac{1}{2}} \right).\end{array}\)

Ta có: \(\overrightarrow {AH}  = \left( {5;\, - 5} \right) = 5\left( {1; - 1} \right).\)

Đường thẳng \(BC\) đi qua \(D\) và vuông góc với \(AH,\) nhận \(\overrightarrow {AH} \) làm VTPT

\( \Rightarrow BC:\,\,\,x - \frac{7}{2} - \left( {y - \frac{1}{2}} \right) = 0 \Leftrightarrow x - y - 3 = 0.\)

Gọi \(B\left( {{x_B};\,\,{x_B} - 3} \right);\,\,C\left( {{x_C};\,\,{x_C} - 3} \right)\) thuộc \(BC.\)

Vì \(D\) là trung điểm của\(BC \Rightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 2{x_D} = 7\\{y_B} + {y_C} = 2{y_D} = 1.\end{array} \right.\)

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {BH}  = \left( {2 - {x_B};\,\,4 - {x_B}} \right)\\\overrightarrow {AC}  = \left( {{x_C} + 3;\,\,{x_C} - 9} \right)\end{array} \right..\)

Lại có: \(\overrightarrow {BH}  \bot \overrightarrow {AC}  \Rightarrow \overrightarrow {BH} .\overrightarrow {AC}  = 0\)

\(\begin{array}{l} \Leftrightarrow \left( {2 - {x_B}} \right)\left( {{x_C} + 3} \right) + \left( {4 - {x_B}} \right)\left( {{x_C} - 9} \right) = 0\\ \Leftrightarrow \left( {2 - x{  _B}} \right)\left( {7 - {x_B} + 3} \right) + \left( {4 - {x_B}} \right)\left( {7 - {x_B} - 9} \right) = 0\\ \Leftrightarrow \left( {2 - {x_B}} \right)\left( {10 - {x_B}} \right) - \left( {4 - {x_B}} \right)\left( {{x_B} + 2} \right) = 0\\ \Leftrightarrow 20 - 12{x_B} + x_B^2 - 8 - 2{x_B} + x_B^2 = 0\\ \Leftrightarrow 2x_B^2 - 14{x_B} + 12 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_B} = 6 \Rightarrow {y_B} = 3\,\, \Rightarrow B\left( {6;\,\,3} \right)\,\,\,\left( {ktm} \right)\\{x_B} = 1 \Rightarrow {y_B} =  - 2 \Rightarrow B\left( {1; - 2} \right)\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Chọn A.