Câu hỏi
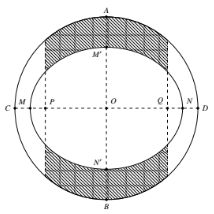
Một khu vườn dạng hình tròn có hai đường kính \(AB,\,\,CD\) vuông góc với nhau, \(AB = 12m\). Người ta làm một hồ cá có dạng hình elip với bốn đỉnh \(M,\,\,N,\,\,M',\,\,N'\) như hình vẽ, biết \(MN = 10m,\)\(M'N' = 8m\), \(PQ = 8m\). Diện tích phần trồng cỏ (phần gạch sọc) bằng:
- A \(20,33{m^2}\)
- B \(33,02{m^2}\)
- C \(23,02{m^2}\)
- D \(32,03{m^2}\)
Phương pháp giải:
+) Đặt trục tọa độ, lập phương trình đường tròn, phương trình elip.
+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
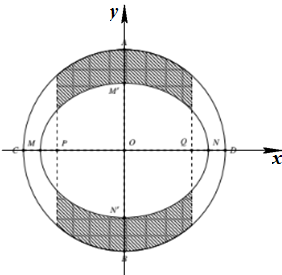
Đặt hệ trục tọa độ như hình vẽ. Ta có \(AB = 12m \Rightarrow OA = 6m\).
Phương trình đường tròn là \({x^2} + {y^2} = 36 \Leftrightarrow y = \pm \sqrt {36 - {x^2}} \).
Phương trình elip là: \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1 \Leftrightarrow y = \pm 4\sqrt {1 - \dfrac{{{x^2}}}{{25}}} \).
Khi đó diện tích phần trồn cỏ là:
\(S = 2\int\limits_{ - 4}^4 {\left( {\sqrt {36 - {x^2}} - 4\sqrt {1 - \dfrac{{{x^2}}}{{25}}} } \right)dx} \approx 32,03\,\,\left( {{m^2}} \right)\).
Chọn D







