Câu hỏi
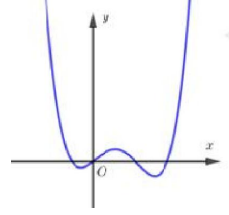
Biết đồ thị hàm số bậc bốn \(y = f\left( x \right)\) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục hoành.
- A 4
- B 0
- C 6
- D 2
Lời giải chi tiết:
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = g\left( x \right)\) và Ox là:
\({\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right) = 0 \Leftrightarrow \dfrac{{f\left( x \right).f''\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{{\left[ {f\left( x \right)} \right]}^2}}} = 0 \Leftrightarrow {\left[ {\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}} \right]^\prime } = 0\), với \(\forall f\left( x \right) \ne 0\)
Đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại 4 điểm phân biệt có hoành độ \({x_1},{x_2},{x_3},{x_4}\)
Giả sử \(f\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\), \(a \ne 0,\,\,{x_1} < {x_2} < {x_3} < {x_4}\)
Ta có: \(f'\left( x \right) = a\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right) + a\left( {x - {x_1}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right) + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_4}} \right) + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\)
\( \Rightarrow \dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = \dfrac{1}{{x - {x_1}}} + \dfrac{1}{{x - {x_2}}} + \dfrac{1}{{x - {x_3}}} + \dfrac{1}{{x - {x_4}}}\)
Ta có: \({\left[ {\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}} \right]^\prime } = 0 \Leftrightarrow \)\( - \left( {\dfrac{1}{{{{\left( {x - {x_1}} \right)}^2}}} + \dfrac{1}{{{{\left( {x - {x_2}} \right)}^2}}} + \dfrac{1}{{{{\left( {x - {x_3}} \right)}^2}}} + \dfrac{1}{{{{\left( {x - {x_4}} \right)}^2}}}} \right) = 0\) : vô nghiệm
Vậy số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục hoành bằng 0.
Chọn: B







