Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên dưới.
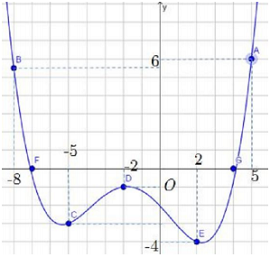
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f\left( {3\sin x + 4\cos x} \right) = f\left( m \right)\) có nghiệm?
- A 10
- B 14
- C 9
- D 11
Phương pháp giải:
Đặt ẩn phụ \(t = 3\sin x + 4\cos x\).
Lời giải chi tiết:
Đặt \(t = 3\sin x + 4\cos x\).
Ta có: \( - \sqrt {{3^2} + {4^2}} \le 3\sin x + 4\cos x \le \sqrt {{3^2} + {4^2}} \Leftrightarrow - 5 \le 3\sin x + 4\cos x \le 5\)\( \Leftrightarrow - 5 \le t \le 5\)
Khi đó, phương trình \(f\left( {3\sin x + 4\cos x} \right) = f\left( m \right)\) có nghiệm \( \Leftrightarrow f\left( t \right) = f\left( m \right)\) có nghiệm trên đoạn \(\left[ { - 5;5} \right]\).
\( \Leftrightarrow - 4 \le f\left( m \right) \le 6 \Leftrightarrow - 8 \le m \le 5\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 8; - 7;...;5} \right\}\): có 14 giá trị.
Chọn: B







