Câu hỏi
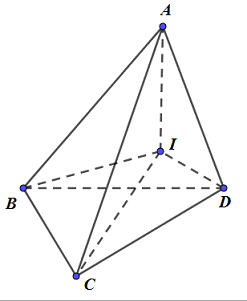
Cho tứ diện ABCD có \(AB = AC = AD = 2a\). Biết tam giác BCD có \(BC = 2a,\,BD = a\), \(\widehat {CBD} = {120^0}\). Tính thể tích tứ diện ABCD theo a.
- A \(\dfrac{{\sqrt 5 }}{3}{a^3}\).
- B \(\dfrac{{\sqrt 5 }}{2}{a^3}\)
- C \(\sqrt 5 {a^3}\).
- D \(\dfrac{{\sqrt 5 }}{6}{a^3}\).
Phương pháp giải:
Sử dụng các công thức diện tích tam giác \(S = \dfrac{1}{2}ab\sin C = \dfrac{{abc}}{{4R}}\) và công thức Cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\).
Lời giải chi tiết:
\({S_{\Delta BCD}} = \dfrac{1}{2}BC.BD.\sin {120^0} = \dfrac{{\sqrt 3 }}{2}{a^2}\)
\(C{D^2} = B{C^2} + B{D^2} - 2BC.BD.\cos {120^0} = 7{a^2} \Rightarrow CD = a\sqrt 7 \).
Ta có: \({S_{\Delta BCD}} = \dfrac{{BC.CD.BD}}{{4R}} \Leftrightarrow \dfrac{{\sqrt 3 }}{2}{a^2} = \dfrac{{2a.a\sqrt 7 .a}}{{4R}} \Leftrightarrow R = \dfrac{{a\sqrt {21} }}{3}\)
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do \(AB = AC = AD \Rightarrow AI \bot \left( {BCD} \right)\)\( \Rightarrow h = AI = \sqrt {A{C^2} - {R^2}} = \dfrac{{a\sqrt {15} }}{3}\)
Thể tích tứ diện ABCD là: \(V = \dfrac{1}{3}.\dfrac{{a\sqrt {15} }}{3}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 5 }}{6}\).
Chọn: D







