Lời giải chi tiết:

Áp dụng BĐT Bunhiacopxki ta có:

\(\begin{array}{l}{\left( {x + y} \right)^2} \le \left( {{1^2} + {1^2}} \right)\left( {{x^2} + {y^2}} \right) = 2\left( {{x^2} + {y^2}} \right)\\ \Rightarrow {\left( {\frac{{{{\left( {x + y} \right)}^2}}}{2}} \right)^2} \le {\left( {\frac{{2\left( {{x^2} + {y^2}} \right)}}{2}} \right)^2} = {\left( {{x^2} + {y^2}} \right)^2} \le 2\left( {{x^4} + {y^4}} \right)\\ \Rightarrow {x^4} + {y^4} \ge \frac{{{{\left( {x + y} \right)}^4}}}{8} = \frac{{{{\left( {3 - z} \right)}^4}}}{8}\end{array}\)

Khi đó ta có: \(P = {x^4} + {y^4} + 8{z^4} \ge \frac{{{{\left( {3 - z} \right)}^4}}}{8} + 8{z^4}\) với \(z \in \left( {0;3} \right)\).

Xét hàm số \(f\left( z \right) = \frac{{{{\left( {3 - z} \right)}^4}}}{8} + 8{z^4}\) trên \(\left( {0;3} \right)\) ta có :

\(\begin{array}{l}f'\left( z \right) = \frac{{ - 4{{\left( {3 - z} \right)}^3}}}{8} + 32{z^3} = 0\\ \Leftrightarrow 64{z^3} = {\left( {3 - z} \right)^3} \Leftrightarrow {\left( {4z} \right)^3} = {\left( {3 - z} \right)^3} \Leftrightarrow 4z = 3 - z \Leftrightarrow z = \frac{3}{5}\end{array}\)

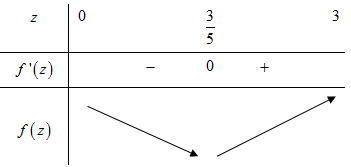
BBT:

Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left( {0;3} \right)} f\left( z \right) = f\left( {\frac{3}{5}} \right) = \frac{{648}}{{125}} = \frac{a}{b} \Rightarrow \left\{ \begin{array}{l}a = 648\\b = 125\end{array} \right. \Rightarrow a - b = 523\).

Chọn B.