Câu hỏi
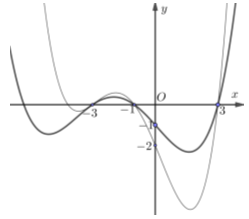
Cho hai hàm số đa thức bậc bốn \(y = f(x)\) và \(y = g(x)\) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số \(y = f(x)\). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là \( - 3\) và cắt nhau tại hai điểm nữa có hoành độ lần lượt là \( - 1\) và \(3\). Tìm tập hợp tất cả các giá trị thực của tham số \(m\) để bất phương trình \(f(x) \ge g(x) + m\) nghiệm đúng với mọi \(x \in {\rm{[}} - 3;3]\).
- A \(\left( { - \infty ;\frac{{12 - 8\sqrt 3 }}{9}} \right]\).
- B \(\left[ {\frac{{12 - 10\sqrt 3 }}{9}; + \infty } \right)\).
- C \(\left( { - \infty ;\frac{{12 - 10\sqrt 3 }}{9}} \right]\).
- D \(\left[ {\frac{{12 - 8\sqrt 3 }}{9}; + \infty } \right)\).
Phương pháp giải:
+) Xác định hàm số \(h\left( x \right) = f\left( x \right) - g\left( x \right)\).
+) \(h\left( x \right) \ge m\,\,\forall x \in \left[ { - 3;3} \right] \Rightarrow m \le \mathop {min}\limits_{\left[ { - 3;3} \right]} h\left( x \right)\).
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy \(f\left( x \right) - g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\,\,\left( {boi\,\,2} \right)\\x = - 1\\x = 3\end{array} \right.\)
Khi đó \(f\left( x \right) - g\left( x \right)\) được viết dưới dạng \(h\left( x \right) = a{\left( {x + 3} \right)^2}\left( {x + 1} \right)\left( {x - 3} \right)\,\,\left( {a \ne 0} \right)\).
Ta có: \(f\left( 0 \right) = - 1;\,\,g\left( 0 \right) = - 2 \Rightarrow f\left( 0 \right) - g\left( 0 \right) = 1\)
\( \Rightarrow - 27a = 1 \Leftrightarrow a = - \frac{1}{{27}} \Leftrightarrow h\left( x \right) = - \frac{1}{{27}}\left( {{x^4} + 4{x^3} - 6{x^2} - 36x - 27} \right)\)
\(\begin{array}{l}f(x) \ge g(x) + m\,\,\forall x \in \left[ { - 3;3} \right] \Leftrightarrow f\left( x \right) - g\left( x \right) \ge m\,\,\forall x \in \left[ { - 3;3} \right]\\ \Rightarrow m \le \mathop {\min }\limits_{\left[ { - 3;3} \right]} h\left( x \right),\,\,h\left( x \right) = f\left( x \right) - g\left( x \right) = - \frac{1}{{27}}\left( {{x^4} + 4{x^3} - 6{x^2} - 36x - 27} \right)\end{array}\)
Ta có \(h'\left( x \right) = \frac{1}{{27}}\left( {4{x^3} + 12{x^2} - 12x - 36} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = \sqrt 3 \\x = - \sqrt 3 \end{array} \right.\)
\(h\left( { - 3} \right) = 0,\,\,\,h\left( 3 \right) = 0,\,\,\,h\left( {\sqrt 3 } \right) = \frac{{12 + 8\sqrt 3 }}{9};\,\,h\left( { - \sqrt 3 } \right) = \frac{{12 - 8\sqrt 3 }}{9}\).
\( \Rightarrow \mathop {\min }\limits_{\left[ { - 3;3} \right]} h\left( x \right) = \frac{{12 - 8\sqrt 3 }}{9} \Leftrightarrow m \le \frac{{12 - 8\sqrt 3 }}{9}\).
Chọn A.