Câu hỏi
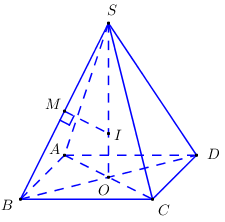
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(BD = 2a\). Tam giác \(SAC\) vuông cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối cầu ngoại tiếp hình chóp \(S.ABCD\) là
- A \(\frac{{4\pi {a^3}}}{3}\).
- B \(4\pi {a^3}\sqrt 3 \).
- C \(\pi {a^3}\).
- D \(4\pi {a^3}\).
Phương pháp giải:
+) Xác định tâm mặt cầu ngoại tiếp.
+) Thể tích khối cầu bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow O\) là trung điểm của \(AC\).
\(\Delta SAC\) cân tại \(S \Rightarrow SO \bot AC\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {ABCD} \right)\\\left( {SAC} \right) \cap \left( {ABCD} \right) = AC\\\left( {SAC} \right) \supset SO \bot AC\end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right)\).
Gọi \(M\) là trung điểm của \(SB\), trong \(\left( {SBD} \right)\) kẻ đường thẳng vuông góc với \(SB\) cắt \(SO\) tại \(I\) \( \Rightarrow IS = IB\).
Lại có \(I \in SO \Rightarrow IA = IB = IC = ID\).
\( \Rightarrow IA = IB = IC = ID = IS \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABCD\).
\(ABCD\) là hình vuông nên \(AC = BD = 2a\) , mà tam giác \(SAC\) vuông cân tại \(S\) suy ra \(SA = SC = \frac{{AC}}{{\sqrt 2 }} = a\sqrt 2 \).
Xét tam giác vuông \(SOA:\,\,SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {2{a^2} - {a^2}} = a\).
Xét tam giác vuông \(SOB:\,\,SB = \sqrt {S{O^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
Dễ dàng chứng minh được \(\Delta SIM \sim \Delta SBO\,\,\left( {g.g} \right) \Rightarrow \frac{{SI}}{{SB}} = \frac{{SM}}{{SO}} \Rightarrow SI = \frac{{SM.SB}}{{SO}} = \frac{{\frac{{a\sqrt 2 }}{2}.a\sqrt 2 }}{a} = a = R\).
Vậy thể tích khối cầu ngoại tiếp chóp là \(V = \frac{4}{3}\pi {a^3}\).
Chọn A.