Lời giải chi tiết:

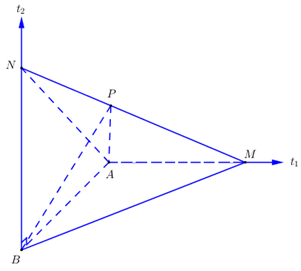
Ta có: \(A{t_1},\,\,B{t_2}\) tiếp xúc với mặt cầu \( \Rightarrow A{t_1} \bot AB,\,\,B{t_2} \bot AB\).

Có: \(\left\{ \begin{array}{l}AM \bot AB\\AM \bot BN\end{array} \right. \Rightarrow AM \bot \left( {ABN} \right) \Rightarrow AM \bot AN \Rightarrow \Delta AMN\) vuông tại A.

Gọi \(P\) là điểm tiếp xúc của \(MN\) với \(\left( S \right)\), áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: \(\left\{ \begin{array}{l}NB = NP\\MP = MA\end{array} \right.\).

Xét tam giác vuông \(AMN:\,\,A{M^2} + A{N^2} = M{N^2}\)

\(\begin{array}{l} \Rightarrow A{B^2} + B{N^2} + A{M^2} = {\left( {NP + MP} \right)^2}\\ \Leftrightarrow 36 + B{N^2} + A{M^2} = {\left( {BN + AM} \right)^2}\\ \Leftrightarrow 36 + B{N^2} + A{M^2} = B{N^2} + A{M^2} + 2BN.AM\\ \Leftrightarrow BN.AM = 18\end{array}\).

\({V_{ABMN}} = {V_{N.ABM}} = \frac{1}{3}.BN.\frac{1}{2}.AB.AM = \frac{1}{6}.6.18 = 18 \in \left( {17;21} \right)\)

Chọn A.