Câu hỏi
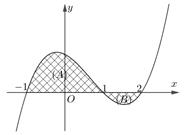
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng \((A),\,(B)\) lần lượt bằng \(15\) và \(3\). Tích phân \(\int\limits_{\frac{1}{{\rm{e}}}}^1 {\frac{1}{{\rm{x}}}{\rm{.f(3lnx}}\,{\rm{ + }}\,{\rm{2)dx}}} \) bằng
- A \(4\)
- B \( - 4\).
- C \( 6\)
- D \( - 6\)
Phương pháp giải:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \)
Sử dụng phương pháp đổi biến để tính tích phân.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta có: \({S_A} = \int\limits_{ - 1}^1 {f\left( x \right)dx} = 15;\,\,\,{S_B} = \int\limits_1^2 {\left( { - f\left( x \right)} \right)dx} = 3.\)
\(I = \int\limits_{\frac{1}{{\rm{e}}}}^1 {\frac{1}{x}{\rm{.}}f\left( {{\rm{3}}\ln x\,{\rm{ + }}\,{\rm{2}}} \right)dx} \)
Đặt \(t = 3\ln x + 2 \Rightarrow dt = \frac{3}{x}dx\)
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 2\\x = \frac{1}{e} \Rightarrow t = 3\ln \frac{1}{e} + 2 = - 1.\end{array} \right.\)
\( \Rightarrow I = \int\limits_{ - 1}^2 {\frac{1}{3}f\left( t \right)dt} = \frac{1}{3}\left[ {\int\limits_{ - 1}^1 {f\left( t \right)dt} + \int\limits_1^2 {f\left( t \right)dt} } \right] = \frac{1}{3}\left[ {\int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} } \right] = \frac{1}{3}\left( {15 - 3} \right) = 4.\)
Chọn A.