Câu hỏi
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng l. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết OM = 8\(\text{ }\!\!\lambda\!\!\text{ }\), ON = 12\(\text{ }\!\!\lambda\!\!\text{ }\) và OM vuông góc với ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
- A 5
- B 4
- C 6
- D 7
Phương pháp giải:
Kẻ OH \(\bot \) MN, từ hệ thức \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{M}^{2}}}+\frac{1}{O{{N}^{2}}}\) tính được OH.
Ta xác định các điểm mà phần tử dao động ngược pha với nguồn trên các đoạn MH và NH. Từ đó rút ra số điểm cần tìm.
Lời giải chi tiết:
Ta có: \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{M}^{2}}}+\frac{1}{O{{N}^{2}}}=\frac{1}{{{\left( 8\lambda \right)}^{2}}}+\frac{1}{{{\left( 12\lambda \right)}^{2}}}\Rightarrow OH=6,66\lambda \)Các điểm dao động ngược pha với O cách O một khoảng \(d=\frac{2k+1}{2}\lambda \)
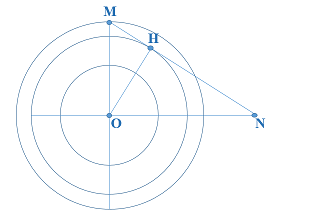
Số điểm nằm trên MH : \(6,66\lambda \le \frac{2k+1}{2}\lambda \le 8\lambda \Rightarrow 6,16\le k\le 7,5\Rightarrow k=7\), có 1 điểm
Số điểm nằm trên NH : \(6,66\lambda \le \frac{2k+1}{2}\lambda \le 12\lambda \Rightarrow 6,16\le k\le 11,5\Rightarrow k=7,8,9,10,11\), có 5 điểm
Tổng số điểm dao động ngược pha với O là: 6
Chọn C







