Phương pháp giải:

Sử dụng phân chia khối đa diện để tính thể tích \(A.BMPN\)

Sử dụng tỉ lệ thể tích: Chóp tam giác \(S.ABC\) có \(M,N,P\) bất kì lần lượt thuộc cạnh \(SA,SB,SC\) suy ra \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}\)

Thể tích khối chóp có chiều cao \(h\) và diện tích đáy \(S\) là \(V = \dfrac{1}{3}h.S\)

Lời giải chi tiết:

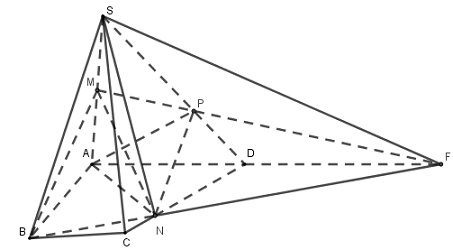
Trong \(\left( {ABCD} \right)\) kéo dài \(BN\) cắt \(AD\) tại \(F.\)

Trong \(\left( {SAD} \right)\) có \(MF \cap SD = \left\{ P \right\}\)

Vì \(BC//DF \Rightarrow \dfrac{{BC}}{{DF}} = \dfrac{{CN}}{{ND}} = \dfrac{1}{3}\)

\( \Rightarrow DF = 3BC \Rightarrow DF = AD\)

Xét tam giác \(SAF\) có \(FM,SD\) là hai đường trung tuyến nên \(P\) là trọng tâm \(\Delta SAD \Rightarrow \dfrac{{SP}}{{SD}} = \dfrac{2}{3}.\)

Ta có \({S_{ABCD}} = \dfrac{{\left( {BC + AD} \right).h}}{2} = 2a.h\)  (với \(BC = a;\,h\) là chiều cao hình thang)

Ta có \({S_{BCN}} = \dfrac{1}{2}d\left( {N,BC} \right).BC = \dfrac{1}{2}a.\dfrac{1}{4}.h = \dfrac{1}{8}ah = \dfrac{1}{{16}}{S_{ABCD}}\)

Tương tự ta có \({S_{AND}} = \dfrac{1}{2}d\left( {N;AD} \right).AD = \dfrac{1}{2}.3a.\dfrac{3}{4}h = \dfrac{9}{8}ah = \dfrac{9}{{16}}{S_{ABCD}}\)

Suy ra \({S_{ABN}} = {S_{ABCD}} - {S_{BCN}} - {S_{ADN}} = {S_{ABCD}} - \dfrac{1}{{16}}{S_{ABCD}} - \dfrac{9}{{16}}{S_{ABCD}} = \dfrac{3}{8}{S_{ABCD}}\)

Từ đó \({V_{S.ABCD}} = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}} = 1\) và \({V_{S.BAN}} = \dfrac{1}{3}.d\left( {S;\left( {BAN} \right)} \right).{S_{BAN}} = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).\dfrac{3}{8}{S_{ABCD}} = \dfrac{3}{8}\)

\({V_{S.ADN}} = \dfrac{1}{3}d\left( {S;\left( {ADN} \right)} \right).{S_{ADN}} = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).\dfrac{9}{{16}}{S_{ABCD}} = \dfrac{9}{{16}}\) 

Lại có \(\dfrac{{{V_{S.MBN}}}}{{{V_{S.ABN}}}} = \dfrac{{SM}}{{SA}} = \dfrac{1}{2} \Rightarrow {V_{S.MBN}} = \dfrac{1}{2}.{V_{S.ABN}}\)  suy ra \({V_{A.MBN}} = \dfrac{1}{2}.\dfrac{3}{8} = \dfrac{3}{{16}}\)

Và \(\dfrac{{{V_{S.MPN}}}}{{{V_{S.ADN}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SP}}{{SD}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3} \Rightarrow {V_{A.MPDN}} = \dfrac{2}{3}.{V_{S.ADN}} = \dfrac{2}{3}.\dfrac{9}{{16}} = \dfrac{3}{8}.\)

\({V_{P.ADN}} = \dfrac{1}{3}d\left( {P,\left( {ADN} \right)} \right).{S_{ADN}} = \dfrac{1}{3}.\dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).\dfrac{9}{{16}}{S_{ABCD}} = \dfrac{3}{{16}}{V_{ABCD}} = \dfrac{3}{{16}}\)

Suy ra \({V_{A.MNP}} = {V_{A.MNDP}} - {V_{P.AND}} = \dfrac{3}{8} - \dfrac{3}{{16}} = \dfrac{3}{{16}}\)

Từ đó \({V_{A.MBNP}} = {V_{A.MNB}} + {V_{A.MNP}} = \dfrac{3}{{16}} + \dfrac{3}{{16}} = \dfrac{3}{8}.\)

Chọn A