Phương pháp giải:

\(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\\left( P \right) \supset a \bot d\\\left( Q \right) \supset b \bot d\end{array} \right. \Rightarrow \angle \left( {\left( P \right);\left( Q \right)} \right) = \angle \left( {a;b} \right)\).

Sử dụng công thức khoảng cách \(h = \dfrac{{3V}}{S}\).

Lời giải chi tiết:

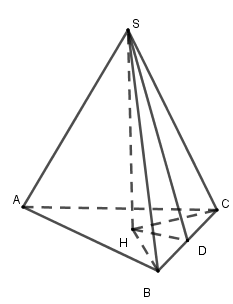
Gọi \(D\) là trung điểm \(BC \Rightarrow HD \bot BD;\,\,HD = \dfrac{{BC}}{2} = \dfrac{a}{2}\) .

Lại có \(\left\{ \begin{array}{l}BC \bot HD\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHD} \right) \Rightarrow BC \bot SD\)

Ta có \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\HD \bot BC,\,SD \bot BC\end{array} \right.\)

\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {HD;SD} \right) = \angle SDH = {60^0}\).

Xét tam giác \(SHD\) vuông tại \(H\) có \(SD = \dfrac{{HD}}{{\cos \widehat {SDH}}} = \dfrac{a}{2}:\dfrac{1}{2} = a\)

Suy ra \({S_{SBC}} = \dfrac{1}{2}SD.BC = \dfrac{{{a^2}}}{2}\)

Ta có \({V_{S.ABC}} = \dfrac{1}{3}d\left( {A,\left( {SBC} \right)} \right).{S_{SBC}} \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{SBC}}}} = \dfrac{{3{a^3}}}{{\dfrac{{{a^2}}}{2}}} = 6a\)

Chọn D