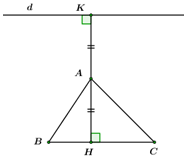
Câu hỏi
Cho \(\Delta ABC\) có \(A\left( {4;\,\,5} \right),\,\,B\left( { - 5; - 2} \right),\,\,C\left( {10;\,\,1} \right).\) Phương trình đường thẳng \(d\) đối xứng với \(BC\) qua \(A\) là:
- A \(x - 5y + 47 = 0\)
- B \(x - 5y + 53 = 0\)
- C \(5x + y - 25 = 0\)
- D \(5x + y + 25 = 0\)
Phương pháp giải:
+) Đường thẳng đối xứng với \(BC\) qua \(A\) song song với \(BC.\)
+) Gọi \(H\) là hình chiếu của \(A\) trên \(BC \Rightarrow \) tọa độ điểm \(H.\)
+) Gọi \(K\) là điểm đối xứng với \(H\) qua \(A \Rightarrow A\) là trung điểm của \(HK \Rightarrow \) tọa độ điểm \(K.\)
\( \Rightarrow d\) là đường thẳng đi qua \(K\) và song song với \(BC.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {BC} = \left( {15;\,\,3} \right) = 3\left( {5;\,\,1} \right)\)
\( \Rightarrow \) đường thẳng \(BC\) đi qua \(B\left( { - 5; - 2} \right)\) và có VTPT \(\overrightarrow n = \left( {1; - 5} \right)\)
\( \Rightarrow BC:\,\,\,\left( {x + 5} \right) - 5\left( {y + 2} \right) = 0 \Leftrightarrow x - 5y - 5 = 0.\)
Phương trình đường thẳng \(\Delta \) đi qua \(A\left( {4;\,\,5} \right)\) và vuông góc với \(BC:\) \(5\left( {x - 4} \right) + y - 5 = 0 \Leftrightarrow 5x + y - 25 = 0.\)
Gọi \(H\) là giao điểm của \(d\) và \(BC \Rightarrow \) tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 5y - 5 = 0\\5x + y - 25 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 0\end{array} \right. \Rightarrow H\left( {5;\,\,0} \right).\)
Gọi \(K\) là điểm đối xứng với \(H\left( {5;\,\,0} \right)\) qua \(A\left( {4;\,\,5} \right) \Rightarrow A\) là trung điểm của \(HK \Rightarrow K\left( {3;\,\,10} \right)\)
\( \Rightarrow d\) là đường thẳng đi qua \(K\left( {3;\,\,10} \right)\) và song song với \(BC\)
\( \Rightarrow d:\,\,\,x - 3 - 5\left( {y - 10} \right) = 0 \Leftrightarrow x - 5y + 47 = 0.\)
Chọn A.