Câu hỏi
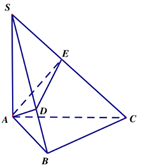
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại B, SA vuông góc với mặt đáy \(\left( {ABC} \right)\), \(BC = a\), góc hợp bởi \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là \({60^0}\). Mặt phẳng \(\left( P \right)\) qua A vuông góc với SC cắt SB, SC lần lượt tại D, E. Thể tích khối đa diện \(ABCED\) là:
- A \(\frac{{{a^3}\sqrt 3 }}{6}\).
- B \(\frac{{11{a^3}\sqrt 3 }}{{120}}\).
- C \(\frac{{11{a^3}\sqrt 3 }}{{60}}\).
- D \(\frac{{3{a^3}\sqrt 3 }}{{40}}\).
Phương pháp giải:
Lập tỉ số thể tích.
Lời giải chi tiết:
\(ABC\) là tam giác vuông cân tại B, \(BC = a\)\( \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}{a^2}\)
Góc hợp bởi \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là \({60^0} \Rightarrow \widehat {SBA} = {60^0} \Rightarrow SA = a.\sqrt 3 \)\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}.SA.{S_{\Delta ABC}} = \frac{{{a^3}\sqrt 3 }}{6}\)
\(\Delta SAB\) có: \(\frac{{S{A^2}}}{{S{B^2}}} = \frac{{SD}}{{SB}}\); \(\Delta SAC\) có: \(\frac{{S{A^2}}}{{S{C^2}}} = \frac{{SE}}{{SC}}\)
\(\frac{{{V_{S.ADE}}}}{{{V_{S.ABC}}}} = \frac{{SD}}{{SB}}.\frac{{SE}}{{SC}} = \frac{{3{a^2}}}{{4{a^2}}}.\frac{{3{a^2}}}{{5{a^2}}} = \frac{9}{{20}}\)\( \Rightarrow {V_{ABCED}} = \frac{{11}}{{20}}{V_{S.ABC}} = \)\(\frac{{11{a^3}\sqrt 3 }}{{120}}\).
Chọn: B