Câu hỏi
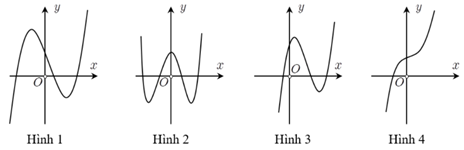
Cho hàm số \(y = {x^3} + b{x^2} + cx + d\) với \(c < 0\) có đồ thị \(\left( C \right)\) là một trong bốn hình dưới đây
Hỏi đồ thị \(\left( C \right)\) là hình nào?
- A Hình 2.
- B Hình 3.
- C Hình 1.
- D Hình 4.
Phương pháp giải:
Nhận biết đồ thị hàm số bậc ba.
Lời giải chi tiết:
\(y = {x^3} + b{x^2} + cx + d\) là hàm số bậc ba \( \Rightarrow \left( C \right)\)không thể là hình 2
\(y' = 3{x^2} + 2bx + c\), ta có: \(c < 0 \Rightarrow 3.c < 0 \Rightarrow \)\(y' = 0\) có 2 nghiệm trái dấu
\( \Rightarrow \) hàm số có hai điểm cực trị nằm về 2 phía của trục tung.
\( \Rightarrow \)Chọn Hình 1.
Chọn: C
Câu hỏi trước
