Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

\(\begin{array}{l}\dfrac{z}{{\sqrt {{a^2} + 1} }} = \dfrac{{i - a}}{{1 - a\left( {a - 2i} \right)}} \Leftrightarrow z = \dfrac{{i - a}}{{1 - {a^2} + 2ai}}\sqrt {{a^2} + 1} \\ \Leftrightarrow z = \dfrac{{i - a}}{{ - {{\left( {a - i} \right)}^2}}}\sqrt {{a^2} + 1}  \Leftrightarrow z = \dfrac{{\sqrt {{a^2} + 1} }}{{a - i}} = \dfrac{{\sqrt {{a^2} + 1} \left( {a + i} \right)}}{{{a^2} - {i^2}}}\\ \Leftrightarrow z = \dfrac{{\sqrt {{a^2} + 1} \left( {a + i} \right)}}{{{a^2} + 1}} \Leftrightarrow z = \dfrac{{a + i}}{{\sqrt {{a^2} + 1} }} = \dfrac{a}{{\sqrt {{a^2} + 1} }} + \dfrac{1}{{\sqrt {{a^2} + 1} }}i\end{array}\)

\(M\) là điểm biểu diễn số phức \(z \Rightarrow M\left( {\dfrac{a}{{\sqrt {{a^2} + 1} }};\dfrac{1}{{\sqrt {{a^2} + 1} }}} \right)\).

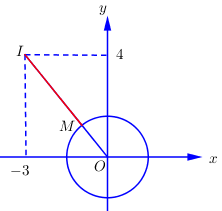
Ta có \({\left( {\dfrac{a}{{\sqrt {{a^2} + 1} }}} \right)^2} + {\left( {\dfrac{1}{{\sqrt {{a^2} + 1} }}} \right)^2} = \dfrac{{{a^2} + 1}}{{{a^2} + 1}} = 1 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \({x^2} + {y^2} = 1\) có tâm \(O\left( {0;0} \right)\) bán kính \(R = 1\).

Khi đó \(I{M_{\min }} = IO - R = \sqrt {{{\left( { - 3} \right)}^2} + {4^2}}  - 1 = 5 - 1 = 4\).

Chọn A