Phương pháp giải:

Sử dụng phương pháp tọa độ hóa.

Lời giải chi tiết:

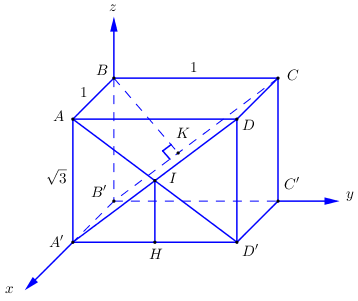
Chọn \(a = 1\). Gắn hệ trục tọa độ như hình vẽ.

Ta có \(B'\left( {0;0;0} \right),\,\,A'\left( {1;0;0} \right),\,A\left( {1;0;\sqrt 3 } \right);\,\,\,D'\left( {1;1;0} \right);\,\,B\left( {0;0;\sqrt 3 } \right);\,\,C\left( {0;1;\sqrt 3 } \right)\).

\(I\) là trung điểm của \(AD' \Rightarrow I\left( {1;\dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\).

\(H\) là hình chiếu của \(I\) trên mặt phẳng \(\left( {A'B'C'D'} \right) \Rightarrow H\)là trung điểm của \(A'D' \Rightarrow H\left( {1;\dfrac{1}{2};0} \right)\).

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {CA'}  = \left( {1; - 1; - \sqrt 3 } \right)\\\overrightarrow {CB'}  = \left( {0; - 1; - \sqrt 3 } \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {CA'} ;\overrightarrow {CB'} } \right] = \left( {0;\sqrt 3 ; - 1} \right)\).

Phương trình mặt phẳng \(\left( {CA'B'} \right):\,\,\sqrt 3 y - z = 0\).

Phương trình \(BK\) đi qua \(B\) và vuông góc với \(\left( {CA'B'} \right)\) là: \(\left\{ \begin{array}{l}x = 0\\y = \sqrt 3 t\\z = \sqrt 3  - t\end{array} \right. \Rightarrow K\left( {0;\sqrt 3 t;\sqrt 3  - t} \right)\).

\(K \in \left( {CA'B'} \right) \Rightarrow \sqrt 3 .\sqrt 3 t - \sqrt 3  + t = 0 \Leftrightarrow 4t = \sqrt 3  \Leftrightarrow t = \dfrac{{\sqrt 3 }}{4}\).

\( \Rightarrow K\left( {0;\dfrac{3}{4};\dfrac{{3\sqrt 3 }}{4}} \right)\).

Ta có \(\left\{ \begin{array}{l}\overrightarrow {IH}  = \left( {0;0;\dfrac{{ - \sqrt 3 }}{2}} \right)\\\overrightarrow {IB}  = \left( { - 1;\dfrac{{ - 1}}{2};\dfrac{{\sqrt 3 }}{2}} \right)\\\overrightarrow {IK}  = \left( { - 1;\dfrac{1}{4};\dfrac{{\sqrt 3 }}{4}} \right)\end{array} \right. \Rightarrow {V_{IHBK}} = \dfrac{1}{6}\left| {\left[ {\overrightarrow {IH} ;\overrightarrow {IB} } \right].\overrightarrow {IK} } \right| = \dfrac{1}{6}\left| {\dfrac{{ - \sqrt 3 }}{4}.\left( { - 1} \right) + \dfrac{{\sqrt 3 }}{2}.\dfrac{1}{4} + 0} \right| = \dfrac{{\sqrt 3 }}{{16}}\)

Chọn C