Câu hỏi
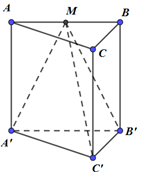
Khối lăng trụ tam giác \(ABC.A'B'C'\), \(M\) là trung điểm của cạnh \(AB\). Trong các khẳng định sau, khẳng định nào sai?
- A \({V_{ABCC'}} = {V_{A'BCC'}}\).
- B \({V_{MA'B'C'}} = {V_{A'ABC}}\).
- C \({V_{A'BCC'}} = {V_{MA'B'C'}}\).
- D \({V_{MA'B'C'}} = \frac{1}{2}{V_{AA'B'C'}}\).
Phương pháp giải:
Lập tỉ số thể tích.
Lời giải chi tiết:
Ta có:
\({V_{ABCC'}} = \frac{1}{3}{V_{ABC.A'B'C'}};\,\,{V_{A'BCC'}} = \frac{1}{2}{V_{A'.BCC'B'}} = \frac{1}{2}.\frac{2}{3}{V_{ABC.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}}\)
\( \Rightarrow {V_{ABCC'}} = {V_{A'BCC'}} \Rightarrow A\) đúng
\({V_{MA'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}};\,\,{V_{A'ABC}} = \frac{1}{3}{V_{ABC.A'B'C'}} \Rightarrow {V_{MA'B'C'}} = {V_{A'ABC}} \Rightarrow B\) đúng
\({V_{A'BC'C}} = \frac{1}{2}{V_{A'.BCC'B'}} = \frac{1}{2}.\frac{2}{3}.{V_{ABC.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}};\,\,\,{V_{MA'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}}\)
\( \Rightarrow {V_{A'BC'C}} = {V_{MA'B'C'}} \Rightarrow C\) đúng
\({V_{MA'B'C'}} = \frac{1}{3}{V_{AA'B'C'}} \Rightarrow D\) sai.
Chọn: D
Câu hỏi trước
