Câu hỏi
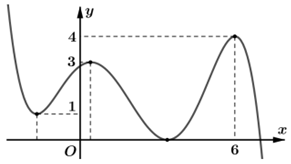
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ. Các giá trị của tham số \(m\) để phương trình \(\frac{{4{m^3} + m}}{{\sqrt {2{f^2}\left( x \right) + 5} }} = {f^2}\left( x \right) + 3\) có ba nghiệm phân biệt là
- A \(m = \pm \frac{{\sqrt {37} }}{2}\)
- B \(m = \frac{{\sqrt 3 }}{2}\)
- C \(m = \frac{{\sqrt 37 }}{2}\)
- D \(m = \pm \frac{{\sqrt {3} }}{2}\)
Phương pháp giải:
Biến đổi để sử dụng với \(f\) là hàm đơn điệu trên \(K\) thì \(f\left( u \right) = f\left( v \right) \Leftrightarrow u = v\)
Từ đó sử dụng đồ thị hàm số đã cho và sự tương giao của hai đồ thị để biện luận số nghiệm của phương trình.
Lời giải chi tiết:
Ta có \(\frac{{4{m^3} + m}}{{\sqrt {2{f^2}\left( x \right) + 5} }} = {f^2}\left( x \right) + 3\) \( \Leftrightarrow 4{m^3} + m = \left( {{f^2}\left( x \right) + 3} \right)\sqrt {2{f^2}\left( x \right) + 5} \)
\(\begin{array}{l} \Leftrightarrow 8{m^3} + 2m = \left( {2{f^2}\left( x \right) + 6} \right)\sqrt {2{f^2}\left( x \right) + 5} \\ \Leftrightarrow {\left( {2m} \right)^3} + 2m = \left( {2{f^2}\left( x \right) + 5} \right)\sqrt {2{f^2}\left( x \right) + 5} + \sqrt {{f^2}\left( x \right) + 5} \left( * \right)\end{array}\)
Xét hàm số \(g\left( t \right) = {t^3} + t\,\) có \(g'\left( t \right) = 3{t^2} + 1 > 0;\,\forall t \Rightarrow g\left( t \right)\) là hàm đồng biến trên \(\mathbb{R}.\)
Phương trình (*) suy ra \(g\left( {2m} \right) = g\left( {\sqrt {2{f^2}\left( x \right) + 5} } \right) \Leftrightarrow \sqrt {2{f^2}\left( x \right) + 5} = 2m\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\2{f^2}\left( x \right) + 5 = 4{m^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{f^2}\left( x \right) = \frac{{4{m^2} - 5}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \frac{{\sqrt 5 }}{2}\\\left[ \begin{array}{l}f\left( x \right) = \sqrt {\frac{{4{m^2} - 5}}{2}} \left( 1 \right)\\f\left( x \right) = - \sqrt {\frac{{4{m^2} - 5}}{2}} \left( 2 \right)\end{array} \right.\end{array} \right.\)
(Vì \(f\left( x \right) = 0\) chỉ có hai nghiệm phân biệt nên \(m > \frac{{\sqrt 5 }}{2}\))
+ Vì \( - \sqrt {\frac{{4{m^2} - 5}}{2}} < 0\) nên từ đồ thị hàm số ta thấy phương trình \(f\left( x \right) = - \sqrt {\frac{{4{m^2} - 5}}{2}} \) có một nghiệm duy nhất.
Từ ycbt suy ra phương trình \(f\left( x \right) = \sqrt {\frac{{4{m^2} - 5}}{2}} \) có hai nghiệm phân biệt
+ Vì \(\sqrt {\frac{{4{m^2} - 5}}{2}} > 0\) nên từ đồ thị hàm số suy ra \(\sqrt {\frac{{4{m^2} - 5}}{2}} = 4 \Leftrightarrow 4{m^2} - 5 = 32 \Leftrightarrow \left[ \begin{array}{l}m = \frac{{\sqrt {37} }}{2}\left( {tm} \right)\\m = - \frac{{\sqrt {37} }}{2}\left( {ktm} \right)\end{array} \right.\)
Chọn C.