Câu hỏi
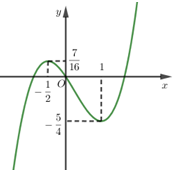
Cho hàm số \(y = {x^3} - \frac{3}{4}{x^2} - \frac{3}{2}x\) có đồ thị như hình vẽ bên. Tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(4\left| {{x^3}} \right| - 3{x^2} - 6\left| x \right| = {m^2} - 6m\) có đúng ba nghiệm phân biệt là
- A \(m = 0\) hoặc \(m = 6\)
- B \(m < 0\) hoặc \(m > 6\)
- C \(0 < m < 3\)
- D \(1 < m < 6\)
Phương pháp giải:
- Dựng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có được từ đồ thị hàm số đã cho bằng cách:
+ Giữ nguyên phần đồ thị bên phải trục \(Oy\).
+ Xóa phần đồ thị phía bên trái trục \(Oy\).
+ Lấy đối xứng phần đồ thị bên phải vừa giữ lại qua \(Oy\).
- Sử dụng tương giao đồ thị suy ra điều kiện của \(m\).
Lời giải chi tiết:
Đặt \(y = f\left( x \right) = {x^3} - \frac{3}{4}{x^2} - \frac{3}{2}x\).
Phương trình \(4\left| {{x^3}} \right| - 3{x^2} - 6\left| x \right| = {m^2} - 6m \Leftrightarrow {\left| x \right|^3} - \frac{3}{4}{x^2} - \frac{3}{2}\left| x \right| = \frac{{{m^2} - 6m}}{4} \Leftrightarrow f\left( {\left| x \right|} \right) = \frac{{{m^2} - 6m}}{4}\)
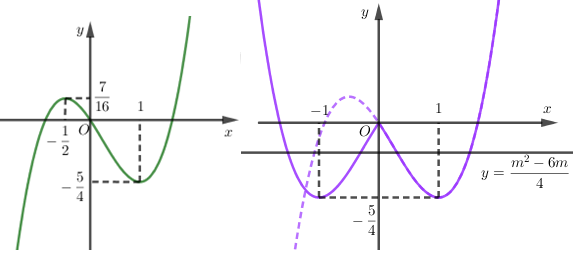
Từ đồ thị hàm số đã cho ta vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau :
Quan sát đồ thị ta thấy, phương trình \(f\left( {\left| x \right|} \right) = \frac{{{m^2} - 6m}}{4}\) có \(3\) nghiệm phân biệt
\( \Leftrightarrow \frac{{{m^2} - 6m}}{4} = 0 \Leftrightarrow {m^2} - 6m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 6\end{array} \right.\).
Chọn A.