Câu hỏi
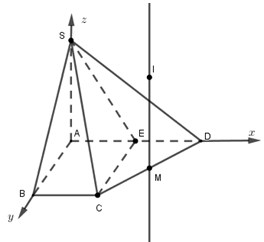
Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với đáy, \(SA = a\sqrt 6 .\) Đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AB = BC = \frac{1}{2}AD = a.\) Gọi \(E\) là trung điểm \(AD.\) Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ECD.\)
- A \(R = \frac{{a\sqrt {30} }}{3}\)
- B \(R = a\sqrt {\frac{{19}}{6}} \)
- C \(R = a\sqrt 6 \)
- D \(R = \sqrt {\frac{{114}}{6}} a\)
Phương pháp giải:
Gắn hệ trục tọa độ, tìm tọa độ các điểm \(S,E,C,D\)
Viết phương trình đường thẳng \(d\) qua \(M\) và song song với \(SA\) (với \(M\) là trung điểm của \(CD\))
Gọi \(I \in d\) để \(I\) là tâm mặt cầu ngoại tiếp \(SECD\) thì \(IS = ID\)
Từ đó tìm được tâm \(I\) và suy ra bán kính mặt cầu.
Lời giải chi tiết:
Vì \(E\) là trung điểm \(AD\) và \(AB = BC = \frac{1}{2}AD = a\) nên \(AB = BC = AE = ED = a\) mà \(BC//AE \Rightarrow \) tứ giác \(ABCE\) là hình vuông suy ra \(CE \bot AD\) hay tam giác \(ECD\) vuông tại \(E\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta ECD\)
Gắn hệ trục tọa độ với \(A \equiv O\left( {0;0;0} \right)\) , \(AD \equiv Ox;\,AB \equiv Oy;AS \equiv Oz\)
Coi đơn vị độ dài là \(a = 1.\)
Suy ra \(A\left( {0;0;0} \right),S\left( {0;0;\sqrt 6 } \right),E\left( {1;0;0} \right),D\left( {2;0;0} \right),C\left( {1;1;0} \right)\) và \(M\left( {\frac{3}{2};\frac{1}{2};0} \right)\) là trung điểm của \(CD.\)
Vì \(\Delta ECD\) vuông tại \(E\) nên taammatwj cầu ngoại tiếp hình chóp \(S.ECD\) thuộc đường thẳng qua \(M\) và song song với \(SA.\)
Phương trình đường thẳng \(d\) qua \(M\) và song song với \(SA\) có 1 VTPT là \(\left( {0;0;1} \right)\) thì có dạng \(d:\left\{ \begin{array}{l}x = \frac{3}{2}\\y = \frac{1}{2}\\z = t\end{array} \right.\)
Suy ra \(I\left( {\frac{3}{2};\frac{1}{2};t} \right)\) là tâm mặt cầu ngoại tiếp chóp \(S.EDC\) thì:
\(\begin{array}{l}IS = ID \Leftrightarrow {\left( {\frac{3}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^2} + {\left( {t - \sqrt 6 } \right)^2} = {\left( { - \frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^2} + {t^2}\\ \Leftrightarrow 2\sqrt 6 t = 8 \Rightarrow t = \frac{4}{{\sqrt 6 }} \Rightarrow I\left( {\frac{3}{2};\frac{1}{2};\frac{4}{{\sqrt 6 }}} \right)\end{array}\)
Bán kính mặt cầu là \(R = ID = \sqrt {{{\left( { - \frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{4}{{\sqrt 6 }}} \right)}^2}} = \sqrt {\frac{{19}}{6}} \)
Hay \(R = \sqrt {\frac{{19}}{6}} a.\)
Chọn B.